Rekurencja¶
W przyrodzie spotykamy obiekty, które są podobne same do siebie - jeśli popatrzymy na cząstkę kalafiora, to wygląda ona prawie tak jak cały kalafior. Ma taką samą strukturę, tylko jest mniejsza.

Rysunki powstające w podobny sposób nazywamy fraktalami. Istnieje wiele znanych fraktali np. płatek Kocha czy trójkąt Sierpińskiego. Do tworzenia ich najczęściej wykorzystujemy rekurencję.

Rekurencja polega na rozwiązywaniu problemu w oparciu o rozwiązania tego samego problemu dla danych o mniejszych rozmiarach. Jeśli umiem rysować kawałek kalafiora, to mogę narysować go całego.
O rozwiązywaniu zadań rekurencyjnych należy myśleć w następujący sposób:
- najpierw szukamy rozwiązania dla najmniejszej możliwej wartości parametru,
- w kolejnym kroku definiujemy rozwiązanie dla dużej wartości parametru za pomocą mniejszych wartości parametru (np. dla parametru n za pomocą rozwiązania dla parametru n - 1).
Warto pamiętać o kilku faktach. Po pierwsze każde zadanie rozwiązane rekurencyjne, można rozwiązać iteracyjnie, czyli za pomocą zwykłych pętli. Po drugie tworząc funkcje rekurencyjne musimy zadbać o tzw. warunek końca. Funkcja rekurencyjna to taka funkcja, która wywołuje samą siebie. Co zatem się stanie, jeśli nie powiemy, kiedy taki ciąg wywołań ma się zakończyć? Zwykle języki programowania są przygotowane na taką sytuację i program jest zatrzymywany, a użytkownik informowany o błędzie - zbyt wiele wywołań rekurencyjnych. Czasem jednak sytuacja jest poważniejsza i zdarza się, że funkcja rekurencyjna może zawiesić działanie komputera.
Liczymy rekurencyjnie¶
Funkcje rekurencyjne możemy wykorzystać do obliczeń lub wypisywania pewnych informacji na ekranie. Często mają one krótszą postać niż analogiczne rozwiązania iteracyjne. Jednak zwykle zajmują więcej pamięci komputera na przechowywanie potrzebnych danych i działają wolniej.
Ćwiczenie 1¶
Poniższe funkcje liczą sumę liczb od 1 do podanej wartości n. Zbadaj ich działanie dla różnych wartości parametru. Czy umiesz wskazać warunek końca?
Ćwiczenie 2¶
Spróbuj napisać funkcję rekurencyjną licząca sumę liczb parzystych od 2 do podanej wartości n. Jaki wynik otrzymasz dla parametru 2? O ile wzrośnie suma, gdy parametr wzrośnie o jeden? Pamiętaj o prawidłowym warunku końca zatrzymującym działanie funkcji.
Rekurencyjne rysunki¶
Tworzenie rekurencyjnych rysunków poznamy na przykładzie pasków i piramid złożonych z kwadratów. Rozwiązanie zadania zaczynamy od zaprojektowania funkcji rysującej np. pasek stopnia 1, później pasek stopnia 2, pasek stopnia 3, itd. Następnie próbujemy wychwycić powtarzające się elementy i przygotować ogólny przepis na rysowanie figury dowolnego stopnia.
Ćwiczenie 3¶
Pasek stopnia n powstaje przez narysowanie kwadratu, przesunięcie żółwia wzdłuż jego boku i powtórzenie tej czynności dla n - 1 pozostałych kwadratów.
Ćwiczenie 4¶
Napisz jednoparametrową funkcję piramida(), po wywołaniu której powstanie rysunek, taki jak poniżej. Parametr określa liczbę poziomów piramidy i może przyjmować wartości od 2 do 16. Długość boku kwadratu wynosi 20.
Wynik dla parametru 2:
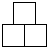
Wynik dla parametru 3:
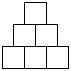
Poniżej znajduje się przykładowe rozwiązanie rekurencyjne tworzące piramidę. Zbadaj działanie funkcji piramida(). Ile kwadratów jest rysowanych dla piramidy stopnia 2? Czym różni się piramida stopnia 4 od piramidy stopnia 3? Zastanów się, jakie poprawki należałoby wprowadzić, by rysować kwadraty o innej długości boku.