Rysujemy płatek Kocha¶

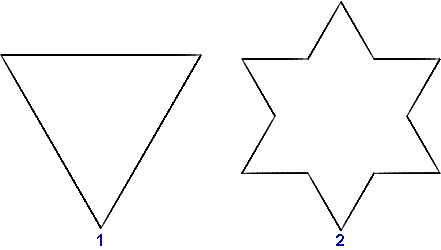
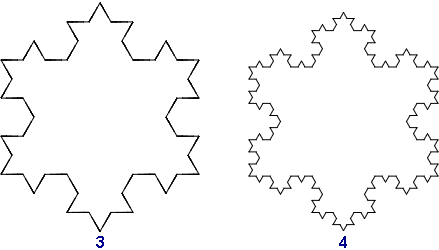
Napisz funkcję o nazwie platek(bok, n), po wywołaniu której powstaną rysunki takie, jak poniżej. Parametr bok określa długość boku płatka, a n stopień złożoności. Odcinki na kolejnych poziomach są trzy razy krótsze, a kąt między nimi wynosi 60°.

Krok po kroku¶

Zastanówmy się, jak powstaje płatek Kocha. Budowany jest on na bazie trójkąta, w którym zamiast boków rysowane są złożone łamane. Zaczynamy rysowanie od jednego boku i stopnia złożoności 1. Będzie to po prostu odcinek.

from turtle import * def koch1(bok): # n będzie zawsze 1 fd(bok) pu(); bk(180); pd() koch1(300)

Teraz koch stopnia 2. Przy definiowaniu dla stopnia 2, korzystamy ze stopnia 1.

from turtle import * def koch1(bok): fd(bok) def koch2(bok): # n będzie zawsze 2 koch1(bok/3) lt(60) koch1(bok/3) rt(120) koch1(bok/3) lt(60) koch1(bok/3) pu(); bk(180); pd() koch2(300)

A jak będzie dla stopnia 3? Czy można to zapisać z wykorzystaniem rozwiązania dla stopnia 2?

from turtle import * def koch1(bok): fd(bok) def koch2(bok): koch1(bok/3) lt(60) koch1(bok/3) rt(120) koch1(bok/3) lt(60) koch1(bok/3) def koch3(bok): # n będzie zawsze 3 koch2(bok/3) lt(60) # tutaj trzeba uzupełnić rt(120) # tutaj trzeba uzupełnić lt(60) # tutaj trzeba uzupełnić pu(); bk(180); pd() koch3(300)

Ogólnie¶

Teraz czas na zapis ogólny. Musimy uzględnić dwa przypadki.

Gdy n = 1, wtedy rysujemy tylko odcinek.

Gdy n > 1, wtedy rysujemy koch stopnia n przy pomocy kocha stopnia n - 1.

from turtle import * def koch_n(bok, n): if n == 1: fd(bok) else: koch_n(bok/3, n-1) lt(60) koch_n(bok/3, n-1) rt(120) # tutaj trzeba dopisać lt(60) koch_n(bok/3, n-1) pu(); bk(180); pd() koch_n(300,4)

Pozostało nam tylko narysować cały płatek Kocha.

from turtle import * def koch_n(bok, n): if n == 1: fd(bok) else: koch_n(bok/3, n-1) lt(60) koch_n(bok/3, n-1) rt(120) koch_n(bok/3, n-1) lt(60) koch_n(bok/3, n-1) def platek(bok, n): pu();bk(180);pd() for i in range(3): koch_n(bok, n) rt(120) tracer(0); platek (200,4); update()

Inne fraktale¶

Proszę teraz samodzielnie napisać funkcję entlik(bok, n), po wywołaniu której powstaną rysunki takie, jak poniżej. Parametr bok określa długość małego odcinka, a n stopień złożoności.

entlik(10, 1)

entlik(10, 2)

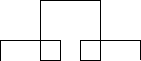
entlik(10, 3)

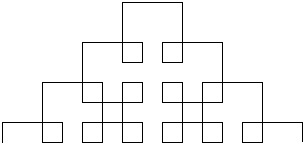
Miejsce na rozwiązanie.

from turtle import * def entlik(bok,n): pass