Nie tylko figury¶
Zastanówmy się, w jaki sposób można wykorzystać instrukcję iteracji do tworzenia różnych rysunków. Zacznijmy od narysowania kwadratu.
for i in range(4):
fd(80); lt(90)
Spróbujmy zamiast odcinka o długości 80 narysować łamaną. W zależności od rodzaju łamanej możemy otrzymać rysunki różniące się bardzo od wyjściowego kwadratu.
Modyfikujemy kwadrat¶
Ćwiczenie 1¶
Poniższy kod spowoduje narysowanie kwadratu. Jedna z linijek została poprzedzona znakiem # oznaczającym komentarz. Usuń ten znak. Jaką figurę otrzymałeś? Jak to wyjaśnić?
Ćwiczenie 2¶
Część linijek została poprzedzona znakiem # oznaczającym komentarz. Usuń ten znak. Jaką figurę otrzymałeś? Jak to wyjaśnić?
Spróbuj zdefiniować inne łamane, zamiast odcinka tworzącego bok kwadratu.
Rysujemy gwiazdki¶
Ćwiczenie 3¶
Naszym zadaniem jest narysowanie trójramiennej gwiazdki:
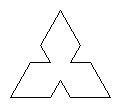
Zmodyfikuj kod tworzący trójkąt równoboczny tak, by otrzymać gwiazdkę.
Zastanówmy się teraz, jak wyliczać kąty, o które obraca się żółw rysując jeżyki.
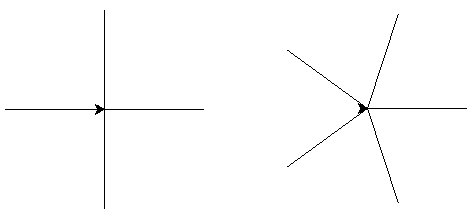
Powyżej dwa przykładowe jeżyki złożone z 4 i 5 odcinków.
Q-9: O jaki kąt powinien obrócić się żółw przy rysowaniu czterech odcinków o wspólnym początku tworzących krzyżyk:
- (A) 45
- Przy takim obrocie między dwoma odcinkami powstanie większy kąt od pozostałych.
- (B) 60
- Przy takim obrocie między dwoma odcinkami powstanie większy kąt od pozostałych.
- (C) 90
- OK.
- (D) 95
- Przy takim obrocie między dwoma odcinkami powstanie mniejszy kąt od pozostałych.
Q-10: Które polecenie wykorzystamy do narysowania pięcioramiennego jeżyka?
- (A) rt(72)
- OK.
- (B) rt(60)
- Powstanie 6 ramion.
- (C) lt(72)
- OK.
- (D) rt(360/5)
- OK, żółw sam może policzyc prawidłowy kąt obrotu.
- (E) lt(71)
- Przy takim obrocie między dwoma odcinkami powstanie większy kąt od pozostałych.
Ćwiczenie 4¶
Rysujemy pięcioramiennego jeżyka złożoną z równomiernie rozmieszczonych odcinków.
Zmień kod w taki sposób, by otrzymać jeżyki o 4, 6, 12 ramionach.